Bea Goller
PhD Architect is also a founder member of Sonic Space Research lab.
Since 2008 she has been researching about the relationship between
sound and architecture (vibration and morphology) and finding interesting
connections between science, art and technology.
She received her PhD, titled Sonic Spaces from the ETSAM in 2015.

Sonic Spaces Research Lab
Researches related on the intersection between sound, space and form
#Sonifications #DataTranslations #Creative Programming #Immersivity
Sound is one of other sensorial layers under explored in architecture due to the predominance of the
visual.
more
Now, translating data processes offer suggestive potentials integrating sonorous layer in design
processes. While sensory layers are implicit in creative architectural design processes,
sound phenomena is a particularly relevant one.
Given the close relationship between sound, space and form, the configuration of a sonorous
dimension might enhance customary architecture as focus on space.
Translations between data, sound, forms and design in the digital domain, are still quite unrevealed.
Such processes can convert sound into a motor of formal genesis, opening up new design paradigms.
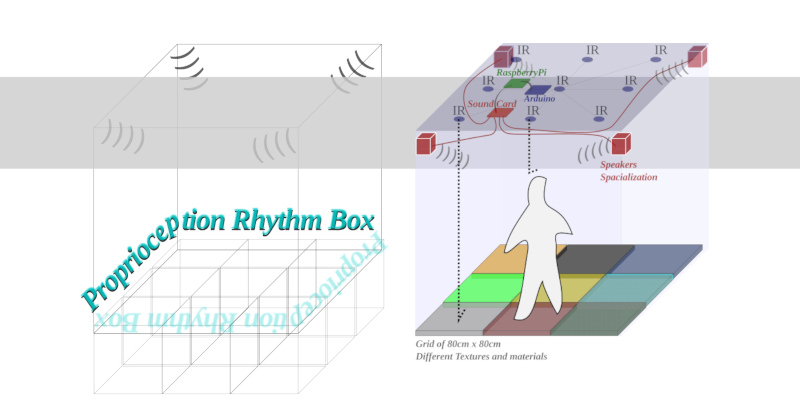
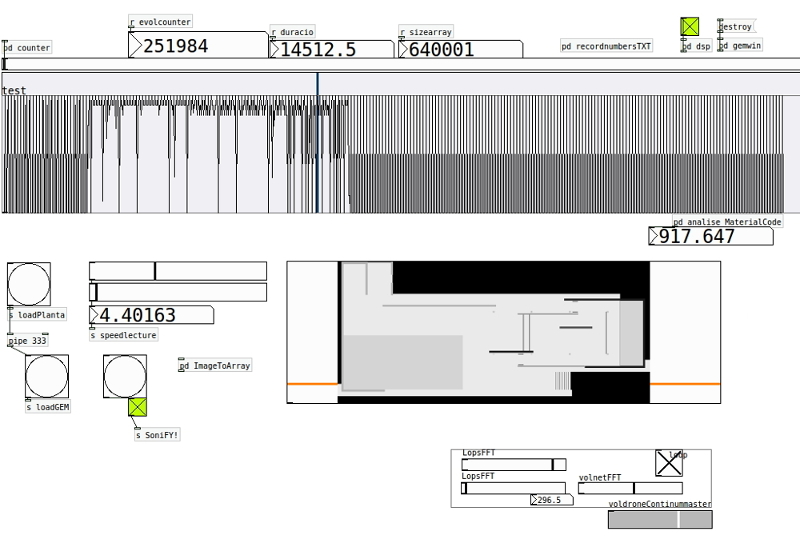
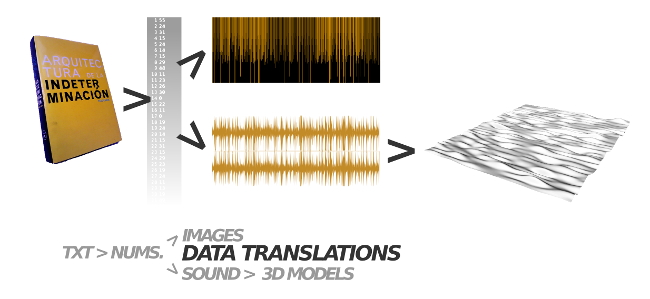
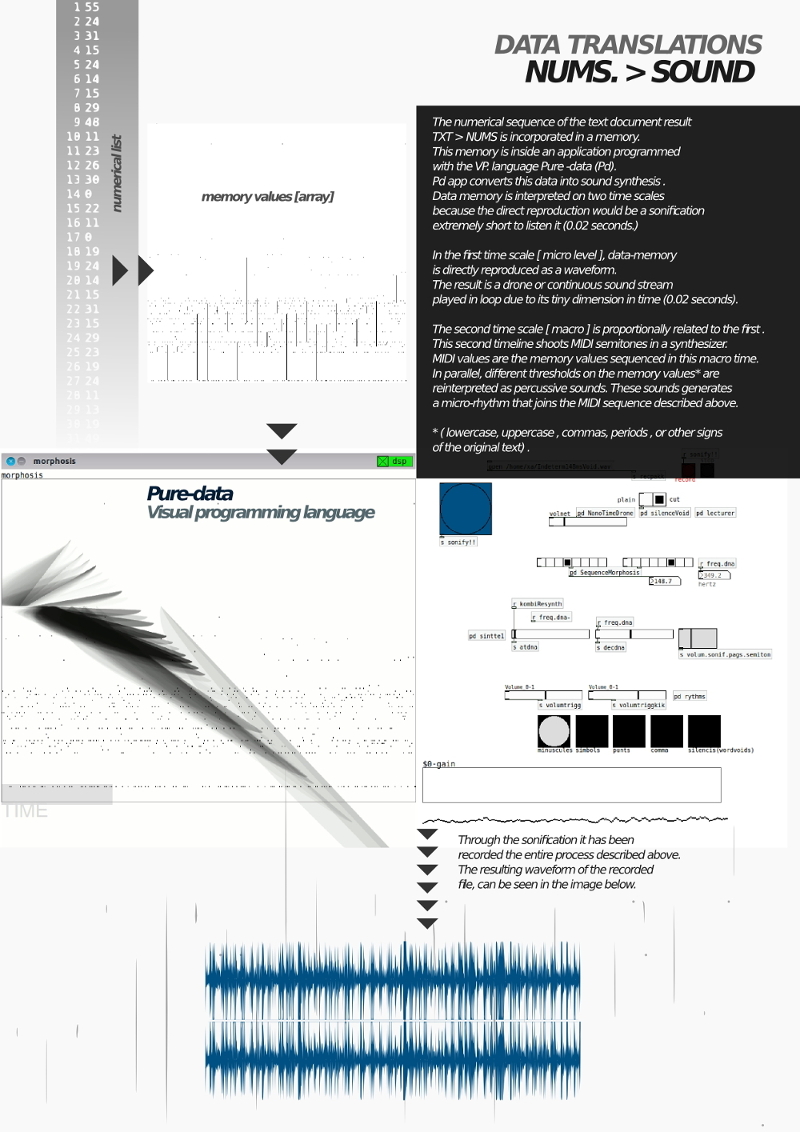
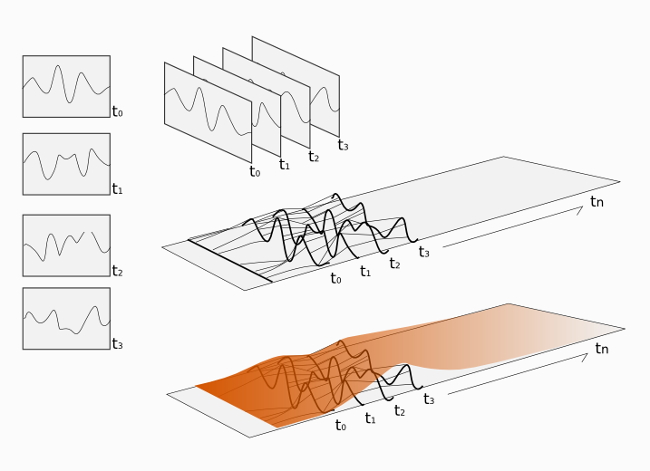
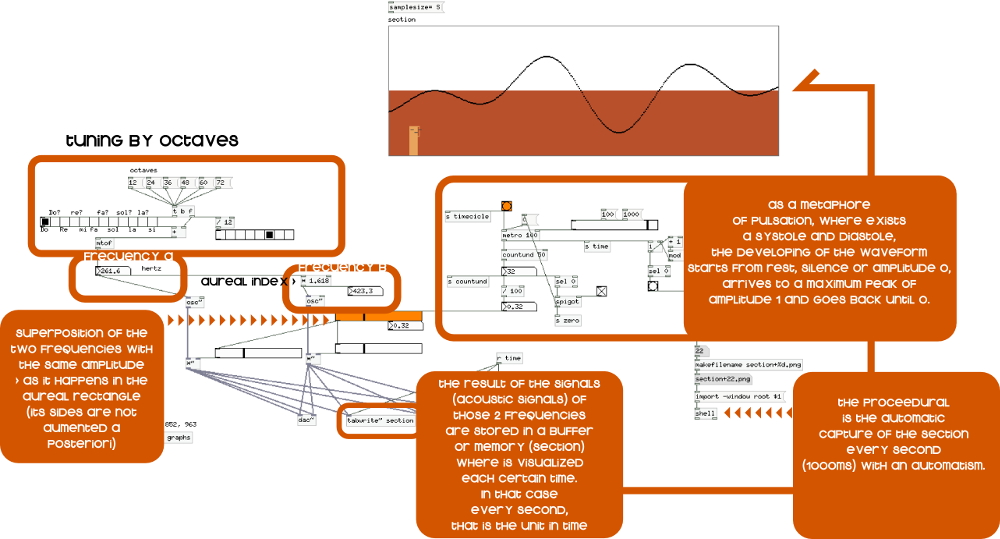
The Sonic space research lab deals about the crossing between morphological form
and sonic vibrations through data translation. This process interprets data by
converting digital entities into others. The most popular of these processes are
sonifications and data visualizations. All these kind of techniques are usually made
through specific coding, connecting these practices with the digital craftmanship. The
digital domain offers many possibilities in creativity, hybridizing different knowledge
fields with multiple sequences, variations and unexpected results. Specific experiments
of data translation are shown, opening up design possibilities and creative techniques.
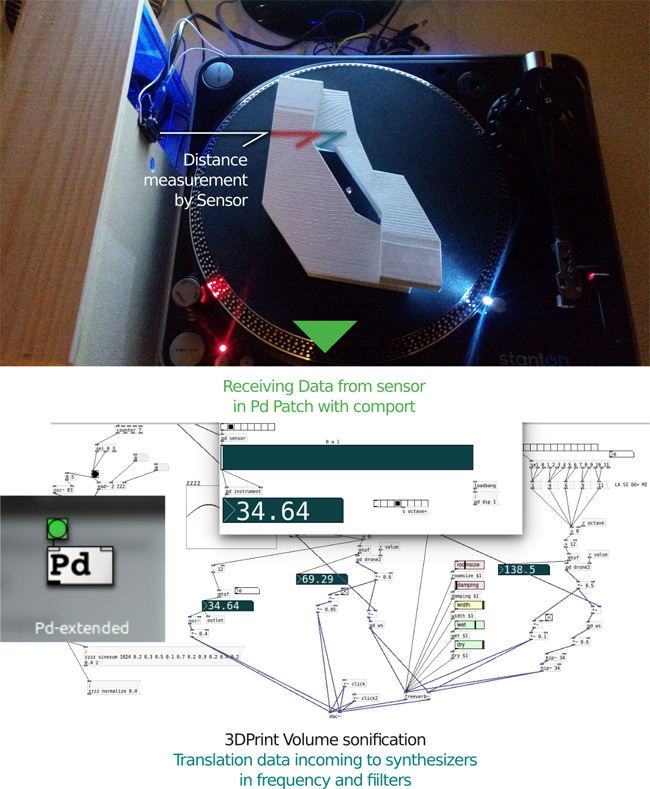
Some of these experiments are produced by means of 3D printing. The goal of this
research is to show how the sound can generate forms and the forms can be heard,
establishing relationships between sound and space. Passing from shape to sound and
from to sound creates an indicating loop about art being a continuous transformation
and that things can have more than one appearance.
The Sonic space research lab deals about the crossing between morphological form and sonic vibrations through data translation. This process interprets data by converting digital entities into others. The most popular of these processes are sonifications and data visualizations. All these kind of techniques are usually made through specific coding, connecting these practices with the digital craftmanship. The digital domain offers many possibilities in creativity, hybridizing different knowledge fields with multiple sequences, variations and unexpected results. Specific experiments of data translation are shown, opening up design possibilities and creative techniques. Some of these experiments are produced by means of 3D printing. The goal of this research is to show how the sound can generate forms and the forms can be heard, establishing relationships between sound and space. Passing from shape to sound and from to sound creates an indicating loop about art being a continuous transformation and that things can have more than one appearance.